5 SORTING ALGORITHMS EVERY PROGRAMMER SHOULD KNOW

Photo by Tyssul Patel on Unsplash

Sorting is the process of arranging the list elements in a specific order and the logic behind this sorting process is referred to as sorting algorithms. The order can be either ascending or descending. If the elements in the list are arranged in increasing order, then the list is sorted in ascending order and if the elements are arranged in decreasing order, then the list is sorted in descending order.

There are several sorting algorithms available and the five most commonly used or popular sorting algorithms are as follows:

• Selection Sort
• Insertion Sort
• Bubble Sort
• Quick Sort
• Merge Sort

Some other sorting algorithms include :

• Shell Sort
• Radix Sort
• Bucket Sort
• Heap Sort

Each above mentioned sorting algorithms differs from one another by logic or by time it takes to sort the elements of the list ( Time Complexity) or by memory used by the algorithms to sort the elements ( Space Complexity)

SELECTION SORT :

Working of Selection Sort

Selection sort sorts the given list of elements by repeatedly finding the minimum element in the list and swaps them with value at the beginning of the list staring from index 0 and so on.

ALGORITHM:

1. By using for loop, loop through index of the list
   for index in range(len(myList))
2. Search for the minimum value of the list.
3. Swap the minimum value with the value at the index position.
4. Repeat the above steps, until the list is sorted.

FLOWCHART :

PROGRAM CODE :

Selection Sort Python Code

To sort the given list in descending order by using selection sort, change the if condition as follows :

if myList[tempIndex] < myList[j] :

ANALYSIS :

Time Complexity : O(n^2)

INSERTION SORT :

Working Of Insertion Sort

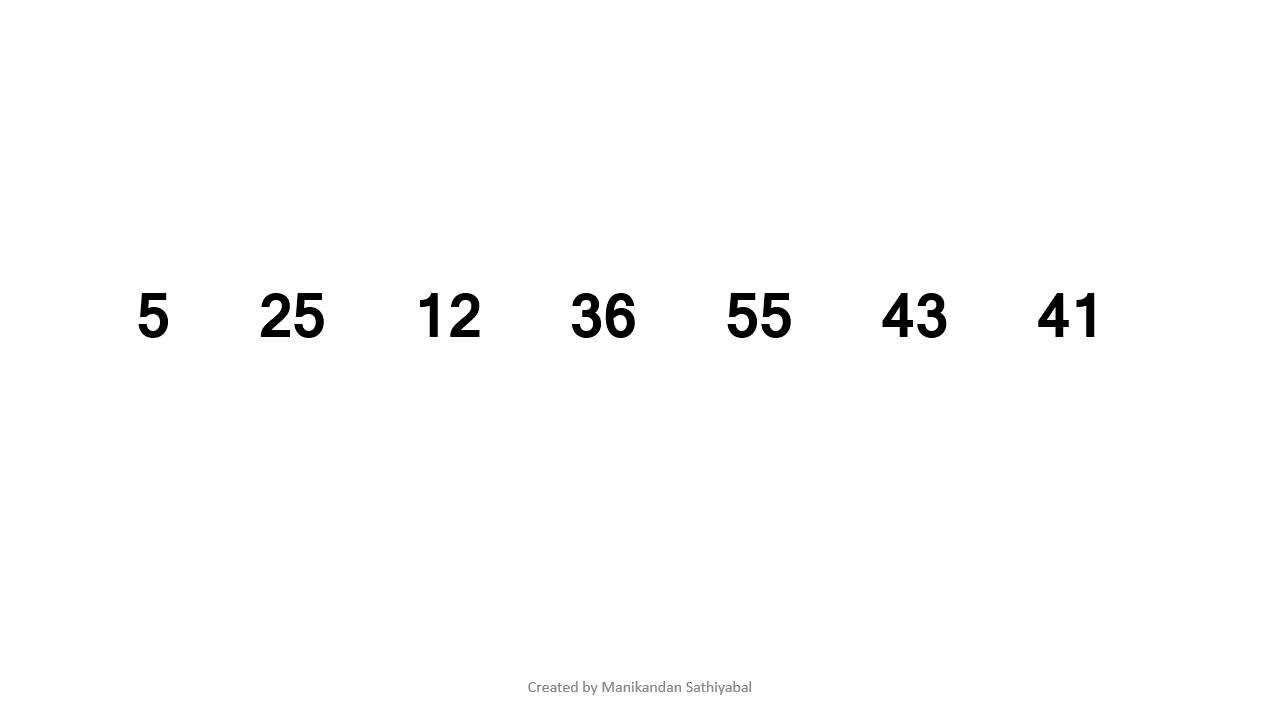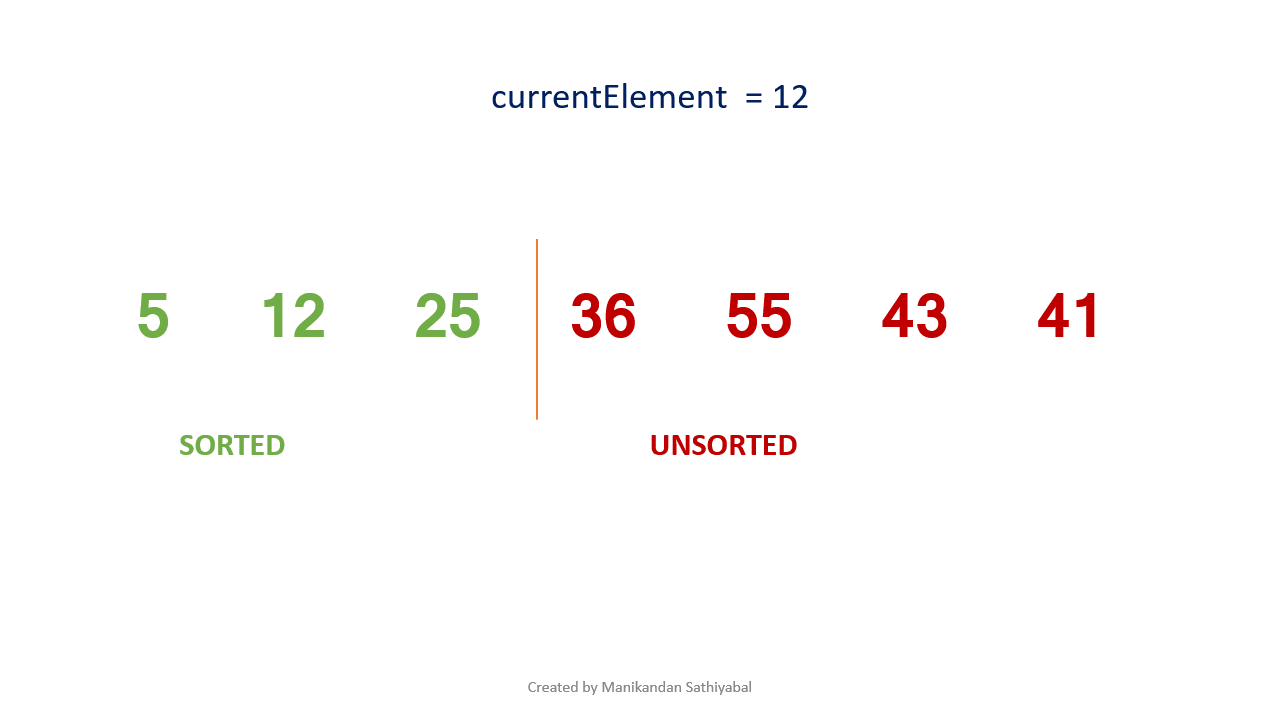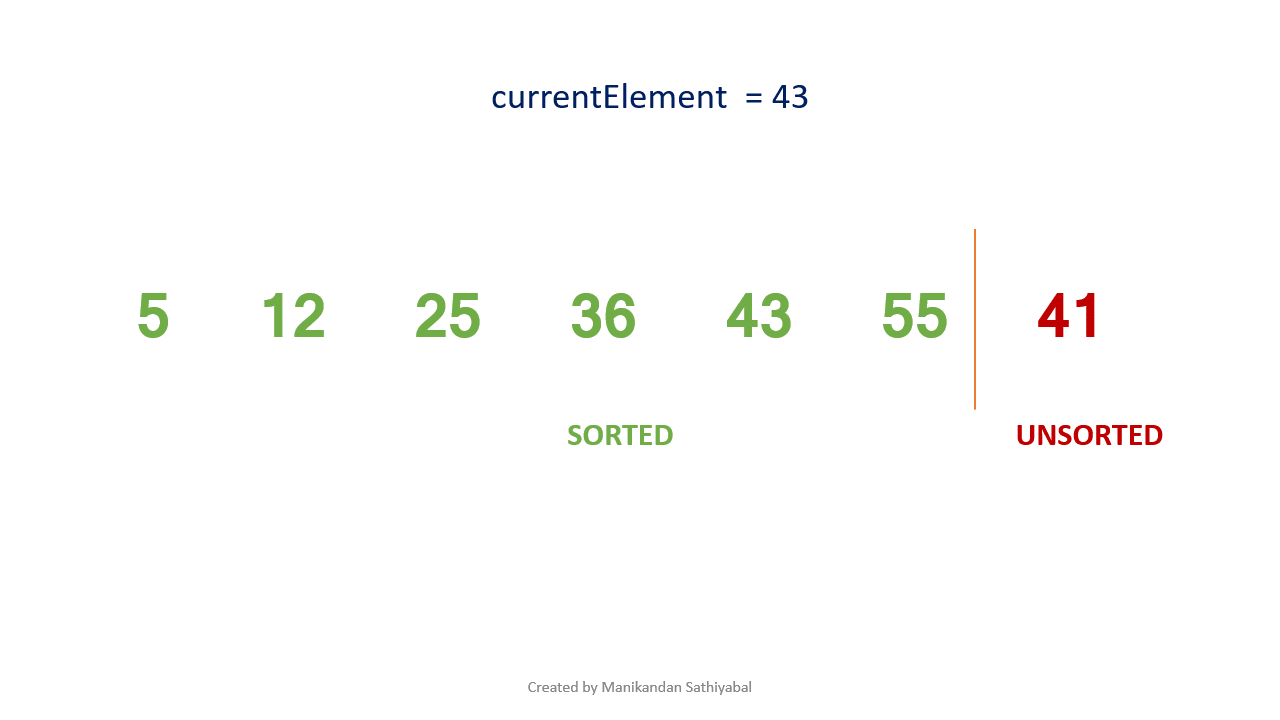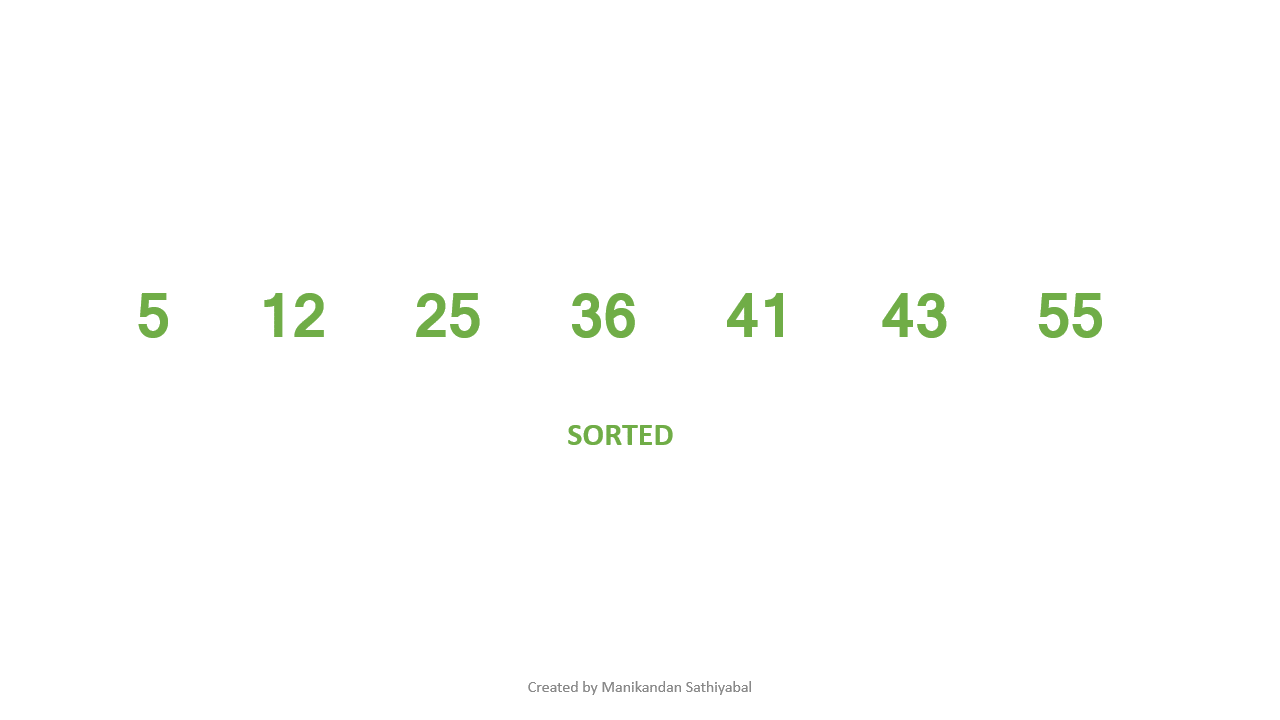
Insertion sort takes an element from the list and places them in the correct index of the list. If the element selected is already in the correct position then skip to the next element.

ALGORITHM:

1. Consider the first value of the list as sorted and remaining values as unsorted.
2. Create a for loop starting from index 1 to length of the list (for looping through all unsorted elements).
3. Get an unsorted value by using for loop and store it in a variable.
4. using while loop , check If unsorted value < sorted values, then move the sorted values to the right and place the unsorted value in the correct index.
5. Repeat the step 4 until all the values in the list are sorted.

FLOWCHART :

Insertion Sort Flowchart

PROGRAM CODE :

Insertion Sort Python Code

The above program code is for sorting elements of the list in ascending order using insertion sort. To sort the list values in descending order, change the while loop condition as follows:

while(currentElement > myList[pos -1] and pos > 0)

ANALYSIS :

Time Complexity : O(n ^2)

BUBBLE SORT :

Working Of Bubble Sort

Bubble Sort algorithm takes an element from the list, compares it with its adjacent element and swaps them if they are in wrong order. If the elements taken are already in correct order, then move to next element of the list.

ALGORITHM:

1. Create a nested for loop, with outer for loop ranges to length of the list. Inner for loop ranges to len(list)-(value of outer for loop)-1 and this is because after one complete iteration of for loop, the last element of the list is sorted.
2. Declare a boolean flag variable and set it to False.
3. By using inner for loop, compare the adjacent elements of the list and swap them if they are in wrong order. Also, set flag variable to True.
4. If the elements are already in correct order, then move to next element of the list.
5. If no elements of the list are swapped, then the list is in sorted order.

FLOWCHART :

Bubble Sort Flow Chart

Bubble Sort Python Code

To sort in descending order by using bubble sort, then change the if condition as follows:

if myList[j] < myList[j+1]

ANALYSIS :

Time Complexity : O(n ^ 2)

QUICK SORT :

Quick Sort splits the list into sub lists and the sub lists are recursively called to sort the elements in the list. Quick sort algorithm follows divide and conquer approach. The name itself tells that quick sort executes faster and is more efficient than its competitor i,e Merge Sort and Heap Sort.

DIVIDE AND CONQUER APPROACH ON QUICK SORT :

DIVIDE :

By using pivot element, the list is divided into sub lists.
The elements smaller then the pivot element are placed on the left and the element greater than the pivot element are placed on the right.

CONQUER :

The left and right sub parts of the list are again divided into sub lists by selecting the pivot elements.

ALGORITHM:

1. Select an element from the list as pivot element.
   Pivot Element can be the :
   1. First element of the list (or)
   2. Last element of the list (or)
   3. Random element of the list (or)
   4. Median of three values
2. Declare and define a function pivotPlace() which returns the correct index of the pivot element.
3. Find the correct index for the pivot element and place it. To do that, three conditions are checked repetitively.
   1. while (leftIndex ≤ rightIndex) and myList[leftIndex] ≤ pivot
   If the above condition satisfies, increment the leftIndex value by 1.
   2.If the above condition fails, then check,
   while (leftIndex ≤ rightIndex) and myList[rightIndex] ≥ pivot
   if this condition satisfies, decrement the rightIndex value by 1
4. If leftIndex > rightIndex, then we get the index of the pivot element.
   The correct pivot index value is :
   rightIndex => if pivot = first element
   leftIndex => if pivot = last element
   else swap the value at leftIndex and rightIndex
5. Partition the list into sub list based on the pivot element. such that the left sub list holds values less than the pivot element and the right sub list holds values that are greater than the pivot element.
6. Declare and define a function QuickSort and call the pivotPlace function. Get the correct index of the pivot element and split the list and recursively call the QuickSort function on the partitioned lists.

FLOW CHART :

Quick Sort Flow Chart

PROGRAM CODE :

In the below program, first element is taken as the pivot element.

Quick Sort Program Code

To sort the values in the descending order, change the condition in the two while loops as follows :

while (left <= right) and myList[left] >= pivot:
    left = left + 1
while (left <= right) and myList[right] <= pivot:
    right = right - 1

To have a better picture on how this algorithm works, check this video.

ANALYSIS :

Time Complexity : O(n ^ 2)

MERGE SORT :

Working Of Merge Sort

Merge sort algorithms is based on Divide and Conquer approach. Merge Sort algorithm divides the list into two sub lists repetitively along the middle value until the sub lists have only one element and then repetitively compares the left and right sub list to sort the elements of the list.

ALGORITHM:

1. Get the index of the middle element by using len(myList)//2 and store it in a variable called mid.
2. Partition the list by using slice operation along the middle element.
   leftList = myList[:mid]
   rightList = myList[:mid]
3. Repeat the above two steps for both leftList and rightList until the leftList and rightList has only one element.
   This can be done by recursively calling the MergeSort function.
4. Now repetitively compare the elements of the leftList and rightList to sort the elements of the list.

Merge Sort Flow Chart

PROGRAM CODE :

To sort the elements of the list in descending order by using merge sort, change the if condition at line 12 as follows :

if leftList[i] > rightList[j] :

ANALYSIS :

Time Complexity : O(nlogn)

CONCLUSION:

I hope this article has helped you understand the five basic sorting algorithm.If you have any doubts/ need clarification please let me know.

You can also find all the images, codes in my Github account here

Good Job, and Thanks for reading.

Happy Coding ❤